What is Geometric Tomography?
Geometric tomography is the area of mathematics dealing with the retrieval of information about a geometric object from data about its sections by lines or planes, or orthogonal projections onto lines or planes, or both. The use of the term "geometric object" is deliberately vague. A special case would be the study of sections or projections of a convex body or polytope, but it is sometimes more appropriate to consider star-shaped bodies, finite sets, compact sets, or even Borel sets.
Within mathematics, geometric tomography has links to convex geometry, integral geometry, Minkowski geometry, functional analysis, and combinatorics, and beyond mathematics, to computerized tomography, discrete tomography, crystallography, electron microscopy, computer vision, morphology, stereology, and pattern recognition.
Context and Notation
While other spaces have been considered, most of the theory concerns subsets of \(n\)-dimensional Euclidean space \(\Bbb{R}^n\) and this is the setting here. The origin in \(\Bbb{R}^n\) is denoted by \(o \) and \(S^{n-1}\) is the unit sphere. If \(x \in \Bbb{R}^n\setminus\{o\}\), then \(x^{\perp}\) is the hyperplane through the origin orthogonal to \(x\). If \(S\) is a subspace (always meaning linear subspace) of \(\Bbb{R}^n\) and \(E\) is a subset of \(\Bbb{R}^n\), then \(E|S\) is the projection (always meaning orthogonal projection) of \(E\) onto \(S\).
Examples
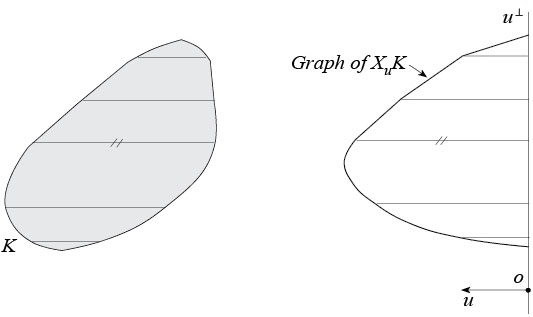
Parallel X-ray of a convex body. The parallel X-ray \(X_uK\) of a convex body \(K\) in \(\Bbb{R}^n\) in the direction \(u\in S^{n-1}\) is the function giving for each \(x\in u^{\perp}\) the length of the intersection of \(K\) with the line through \(x\) parallel to \(u\). In short, \(X_uK\) gives the lengths of all the chords of \(K\) that are parallel to \(u\).
Point or fan-beam X-ray of a convex body. The point X-ray \(X_pK\) of a convex body \(K\) at a point \(p\) in \(\Bbb{R}^n\) is the function giving for each \(u\in S^{n-1}\) the length of the intersection of \(K\) with the line through \(p\) parallel to \(u\). In short, \(X_pK\) gives the lengths of all the chords of \(K\) contained in lines through \(p\).
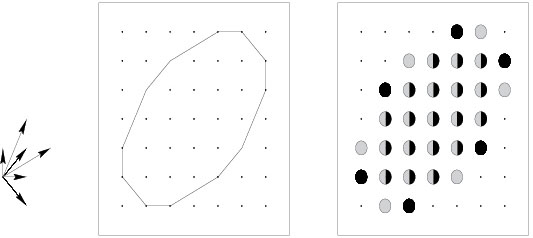
Discrete X-ray of a finite set. The discrete X-ray of a finite subset \(E\) of \(\Bbb{R}^n\) in the direction \(u\in S^{n-1}\) is the function giving for each \(x\in u^{\perp}\) the cardinality of the intersection of \(E\) with the line through \(x\) parallel to \(u\). In short, it gives the number of points in \(E\) lying on each line parallel to \(u\).
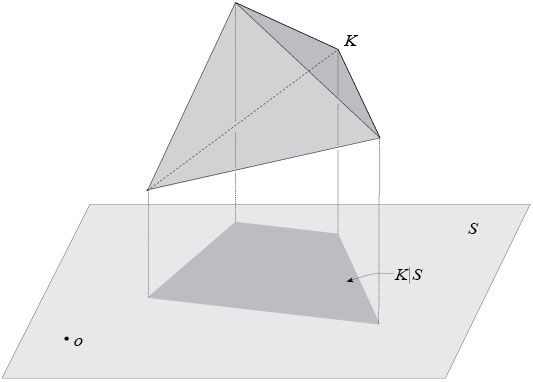
Projection function of a convex body. Suppose that \(i\in \{1,\dots,n-1\}\). The \(i\)th projection function of a convex body \(K\) in \(\Bbb{R}^n\) gives for each \(i\)-dimensional subspace \(S\) in \(\Bbb{R}^n\) the \(i\)-dimensional volume \(V_i(K|S)\) of the projection of \(K\) onto \(S\). In particular, \(i=1\) corresponds to the width function that gives the width of \(K\) in all directions and \(i=n-1\) corresponds to the brightness function that gives the areas (\((n-1)\)-dimensional volumes) of the projections of \(K\) onto hyperplanes.
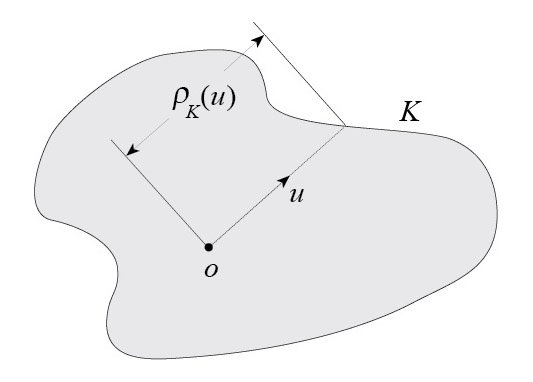
Section function of a star body. Suppose that \(i\in \{1,\dots,n-1\}\). The \(i\)th section function of a star body \(K\) in \(\Bbb{R}^n\) gives for each \(i\)-dimensional subspace \(S\) in \(\Bbb{R}^n\) the \(i\)-dimensional volume \(V_i(K\cap S)\) of the intersection of \(K\) and \(S\). If \(i=n-1\), we simply refer to the section function of \(K\).
Here a star body \(K\) is a set containing the origin and star-shaped with respect to the origin, such that the function giving for each \(u\in S^{n-1}\) the distance from \(o\) to the boundary of \(K\) (called the radial function of \(K\)) is continuous. (Other definitions of the term have been used.)
Theory
To some extent the theory has grown from attempts to solve specific problems. To illustrate, a few of these are described below.
Hammer's X-ray problem. Posed by P. C. Hammer [19] in 1963, this asks how many X-rays are required to permit exact reconstruction of a convex hole in an otherwise homogeneous solid. The question has two parts, depending on whether parallel or point X-rays are used.
Gardner and McMullen [15] gave an answer to the uniqueness aspect of the problem by showing that parallel X-rays of a convex body in \(\Bbb{R}^n\), taken in certain prescribed finite sets of directions, determine the body uniquely among all convex bodies. In fact, when \(n=2\), they completely classified all such "good" sets of directions and showed that any set of four directions for which the cross-ratio of the four corresponding slopes is a transcendental number is a good set. Later, Gardner and Gritzmann [10] found more "practical" good sets of directions, for example, the four directions parallel to the vectors \((1,0)\), \((0,1)\), \((2,1)\), and \((1,-2)\). The best unrestricted uniqueness theorem for point X-rays was established by Volčič [39]: Every set of four noncollinear points in the plane has the property that X-rays of a planar convex body at these points distinguish it from any other such body. Open problems arise when parallel X-rays of convex bodies in \(\Bbb{R}^n\), \(n\ge 3\), are taken in directions in general position, while for point X-rays even the planar case is not fully understood.

Nakajima's problem. An old problem dating back to Nakajima's 1926 paper [30] asks whether any convex body in \(\Bbb{R}^3\) of constant width and constant brightness (that is, whose width and brightness functions are constant) must be a ball. Over the years this question has been the motivation of much work. For example, Goodey, Schneider, and Weil [18] demonstrate that most (in the sense of Baire category) convex bodies in \(\Bbb{R}^n\) are determined, up to translation and reflection in the origin, by their width and brightness functions. The problem was finally solved by Howard [22], who gave an affirmative answer. The same question can be asked for convex bodies in \(\Bbb{R}^n\), \(n\ge 4\), and in this case it is still unsolved (see [23] for further results).
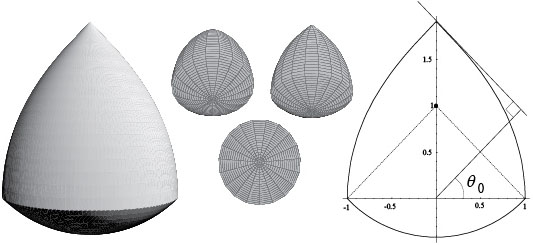
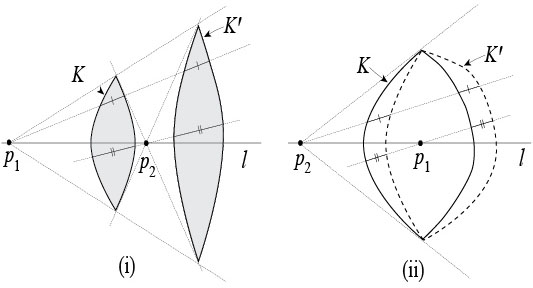
Shephard's problem. In 1964, Shephard [39] asked the following question. Suppose that \(K\) and \(L\) are origin-symmetric (symmetric with respect to the origin) convex bodies in \(\Bbb{R}^n\), such that $$V_{n-1}(K|u^{\perp})\le V_{n-1}(L|u^{\perp}),$$ for each \(u\in S^{n-1}\). Is it true that \(V_n(K)\le V_n(L)\)? In short, must an origin-symmetric body whose shadows have larger areas also have a larger volume? It is easy to see that the answer is affirmative if \(n\le 2\).
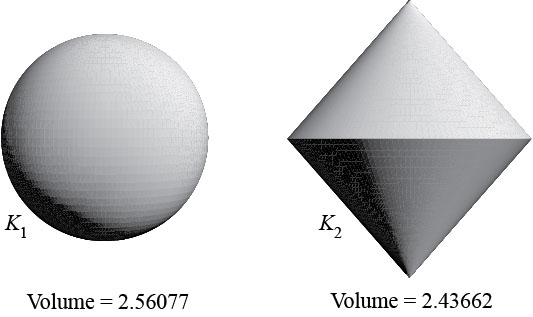
The problem was solved independently by Petty [32] and Schneider [37], both of whom showed that the answer is generally negative if \(n\ge 3\), but affirmative for all \(n\) when \(L\) belongs to a special class of bodies called projection bodies.
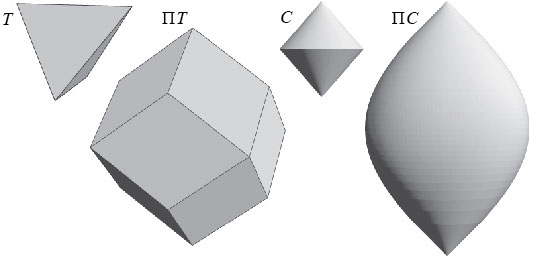
The Busemann-Petty problem. Suppose that \(K\) and \(L\) are origin-symmetric convex bodies in \(\Bbb{R}^n\), such that $$V_{n-1}(K\cap u^{\perp})\le V_{n-1}(L\cap u^{\perp}),$$ for each \(u\in S^{n-1}\). Is it true that \(V_n(K)\le V_n(L)\)? In short, must an origin-symmetric body whose central sections have larger areas also have a larger volume? The question was posed by Busemann and Petty [6] in 1956. It is easy to see that the answer is affirmative if \(n\le 2\).
Lutwak [28] proved that it is also affirmative for all \(n\) when \(K\) belongs to a special class of bodies called intersection bodies. This insight led, after important contributions by several mathematicians (see [9, Note 8.9]) to a unified solution in all dimensions by Gardner, Koldobsky, and Schlumprecht [14]. The answer is affirmative if \(n\le 4\) and negative when \(n\ge 5\).
The equichordal problem. For a long time, one of the oldest unsolved problems in planar geometry was the equichordal problem, posed independently by Fujiwara [8] and Blaschke, Rothe, and Weitzenböck[5]. This asks whether there exists a planar body (that is, a compact convex set in \(\Bbb{R}^2\) equal to the closure of its interior) that contains two different equichordal points. Here, an equichordal point \(p\) in the interior of a body \(E\) is one such that \(E\) is star-shaped with respect to \(p\) and each chord of \(E\) containing \(p\) has the same length. For example, the center of a disk is an equichordal point of it. The book [25, Problem 2] of Klee and Wagon contains an excellent report on the history of the problem up to 1991. Finally, in 1997, Rychlik [36] solved the equichordal problem by showing that no such body exists. The long argument uses invariant manifold theory and some fairly heavy machinery from complex function theory.
The five problems described above form a small part of the extensive theory surveyed more completely in [9]. Inasmuch as part of geometric tomography concerns projections of convex bodies, the Brunn-Minkowski theory from convex geometry provides many tools, including mixed volumes and a plethora of powerful inequalities such as the isoperimetric inequality and its generalizations. The equally effective dual Brunn-Minkowski theory, initiated by Lutwak in 1975, copes with sections of star bodies in a similar way. There is a rich but still quite mysterious interplay between projections of convex bodies and sections (through the origin) of star bodies. Parallel and point X-rays form another important topic. The theory continues to expand and develop, but most of the 66 open problems stated in [9] remain unanswered.
Algorithms
Until the beginning of this century, the mathematical community produced almost no algorithms that served the purpose of geometric tomography. Some algorithms of this type were developed in a program run mainly in the 1980's and 1990's by the electrical engineer Alan Willsky. During the last decade, however, several geometric tomography algorithms have been proposed by mathematicians. Several of these fit into the following general approach:
- For any particular type of data, take measurements of an unknown set \(K\) in a class \(\mathcal{E}\) of sets in \(\Bbb{R}^n\) in a situation for which a full set of exact data determines \(K\) uniquely among all the sets in \(\mathcal{E}\). The measurements should however be realistic: There are available only finitely many noisy measurements, i.e., measurements taken with errors, modeled by the addition of independent random variables with zero mean and fixed variance \(\sigma^2\).
- The task is to design an algorithm that takes \(k\) noisy measurements as input and outputs a set \(P_k\) that approximates \(K\).
- The algorithm should come with a proof of convergence that under suitable, preferably weak, assumptions, for each fixed \(\sigma\) the distance from \(P_k\) to \(K\) converges to 0, almost surely, as
\(k\rightarrow\infty\), in an appropriate metric. If possible, rates of convergence should be obtained. - The algorithm should be implemented and tested.
Reconstruction from surface area measures. An algorithm for the purpose of reconstructing a convex polytope from its surface area measure (effectively, the areas and outer unit normal vectors of its facets) was first published by Little [27]. The algorithm used here is essentially the modification of Little's algorithm proposed by Lemordant, Tao, and Zouaki [26]. It was published by Gardner and Milanfar [16], [17] (see also [9, Section A.4]).
Further information can be found here.
Reconstruction from brightness functions. Aleksandrov's projection theorem [9, Theorem 3.3.1] states that an origin-symmetric convex body \(K\) in \(\Bbb{R}^n\) is uniquely determined, among all such bodies, by its brightness function. Aleksandrov proved this remarkable result - which assumes nothing is known about the shape of the shadows of \(K\), only their areas - in 1937, developing a good deal of the machinery of modern convex geometry in the process. But the theorem does not help with the task of actually reconstructing an origin-symmetric convex body from its brightness function.
Gardner and Milanfar [16], [17] employ a two-stage procedure to effect the reconstruction. By inverting the cosine transform, the first stage reconstructs the surface area measure of \(K\) from its brightness function. The second stage then reconstructs \(K\) from its surface area measure, using the algorithm described in the previous paragraph. Suppose that \((u_i)\) is a sequence of directions dense in \(S^{n-1}\). The algorithm takes as input the brightness function values of \(K\) in the directions \(u_1,\dots,u_k\) and outputs a convex polytope \(P_k\) such that \(P_k\) converges to \(K\) in the Hausdorff metric as \(k\rightarrow\infty\). Though the theoretical results in [17] require exact data, the implemented algorithms already work with noisy data. Gardner, Kiderlen, and Milanfar [13] show that under a weak extra assumption on the sequence \((u_i)\), \(P_k\) still converges, almost surely, to \(K\) as \(k\rightarrow\infty\), and even provide bounds for rates of convergence.
Further information can be found here.
Reconstruction from support functions. The support function of a convex body \(K\) in \(\Bbb{R}^n\) gives for each direction \(u\in S^{n-1}\) the signed distance from \(o\) to the supporting (tangent) hyperplane to \(K\) orthogonal to \(u\). One of the first algorithms arising from Willsky's program was one proposed by Prince and Willsky [33] that reconstructs an approximation to an unknown planar convex body \(K\) from noisy measurements of its support function. There is a very wide multi-disciplinary interest in reconstruction from support functions. See [13] for a long list of references detailing applications to computer tomography, target reconstruction from laser-radar data, and projection magnetic resonance imaging. In view of this, it is surprising that the first convergence proof for the Prince-Willsky algorithm was obtained by Gardner, Kiderlen, and Milanfar [13]. This proof also works for the natural extension of the Prince-Willsky algorithm to higher dimensions.The approach taken by Prince and Willsky encounters obstacles in higher dimensions due to the difficulty in implementing the constraint in their least-squares problem. Gardner and Kiderlen [12] resolve this by a change of variable and develop the first fully satisfactory algorithm for reconstructing 3-dimensional (or higher-dimensional) convex bodies from their support functions.
Further information can be found here.
Reconstruction from covariograms. The covariogram of a convex body \(K\) in \(\Bbb{R}^n\) is the function \(g_K\) defined by \(g_K(x)=V_n\left(K\cap (K+x)\right)\), for \(x \in \Bbb{R}^n\), where \(K+x\) is the translate of \(K\) by the vector \(x\). In short, it gives the volumes of the intersections of \(K\) with its translates. It was introduced around 1975 by G. Matheron , who showed that for a fixed \(u\in S^{n-1}\), the directional derivatives \(\partial g_K(tu)/\partial t\), for all \(t>0\), yield the distribution of the lengths of all chords of \(K\) parallel to \(u\). This explains its relevance to geometric tomography and its utility in fields such as stereology, pattern recognition, and mathematical morphology, where information about an unknown object is to be retrieved from chord length measurements. The covariogram is also important in analytic convex geometry.
Simple to define, the covariogram is notoriously difficult to work with. In 1986, Matheron himself conjectured that planar convex bodies are determined (for the covariogram, the term will always mean up to translation and reflection in the origin) by their covariograms, but this was only recently confirmed by Averkov and Bianchi [1]. Bianchi [2], [3] proved that three-dimensional convex polytopes are determined by their covariograms but in general higher-dimensional ones are not. The uniqueness problem is still open for convex bodies in \(\Bbb{R}^3\).
Bianchi, Gardner, and Kiderlen [4] describe an algorithm for reconstructing convex bodies from their covariograms. The proof of convergence is difficult, depending both on the earlier proof for brightness function reconstruction and new arguments.
Further information can be found here.
Reconstruction from X-rays. The reconstruction aspect of Hammer's X-ray problem is solved by Gardner and Kiderlen [11]. Here, algorithms are given for reconstructing a planar convex body \(K\) from possibly noisy measurements of either its parallel X-rays taken in a fixed finite set of directions or its point X-rays taken at a fixed finite set of points, in known situations that guarantee a unique solution when the data is exact. The algorithms construct a convex polygon \(P_k\) whose X-rays approximate (in the least squares sense) \(k\) equally spaced noisy X-ray measurements of \(K\) in each of the directions or at each of the points. It is shown that these procedures are strongly consistent, meaning that, almost surely, \(P_k\) tends to \(K\) in the Hausdorff metric as \(k\to\infty\).
Further information can be found here.
History
As the above summary of the theory indicates, problems and results that can now be considered as part of geometric tomography have been around for a century or more. However, Richard J. Gardner coined the term at the 1990 Oberwolfach meeting on tomography and made the first systematic attempt to bring its various ingredients together in the first edition of his book with that title in 1995. The scope of the subject in this book owes a great deal to input from Erwin Lutwak in the early 1990's.
It seems that the term geometric tomography was used independently at least twice shortly after 1990. The usage in [32, Chapter 7] has essentially no overlap, but that of Thirion [40] is quite close in spirit; he defines geometric tomography to be the process of reconstructing the external or internal boundaries of objects from their X-rays.
Even earlier, in the 1980's, a program of related research was underway, directed by Alan Willsky, an electrical engineer at MIT. The PhD thesis [35] of Rossi was the first of several supervised by Willsky that develop and implement algorithms specially suited for reconstructing planar convex (and more general) sets. None of these algorithms solve the theoretical problem of obtaining arbitrarily accurate images of convex sets from X-rays in a fixed finite set of directions. However, they do produce images from a limited set of X-rays that are often sufficient for detecting some particular feature of the object, such as the approximate position or orientation of an ellipse or a rectangle. Moreover, they can work even when the data is inaccurate and when noise is present. The general idea is to take advantage of a priori information that the unknown object belongs to a restricted class of homogeneous objects, an idea completely compatible with geometric tomography. As motivation, Rossi gives references for applications to geophysics, oceanography, meteorology, nondestructive testing (locating cracks in nuclear reactor cooling pipes, etc.), and medicine (nearly homogeneous regions such as kidneys and airspaces between organs).
A second edition of the book Geometric Tomography appeared in 2006, with 60 extra pages of text and about 300 additional references. This and other research of Richard Gardner on Geometric Tomography has been supported by the National Science Foundation under grants number DMS-9201508, DMS-9501289, DMS-9802388, DMS-0203527, DMS-0603307, DMS-1103612, and DMS-1402929. Any opinions, findings, and conclusions or recommendations expressed in this material or on this web site are those of the author and do not necessarily reflect the views of the National Science Foundation.
In October, 2005, the first international workshop solely devoted to Geometric Tomography took place in Alicante, Spain, and since then there have been several conferences focusing on Geometric Tomography held in Canada, Denmark, and Italy.
Relation to Computerized Tomography
Most major hospitals have a machine called a CAT (Computerized Axial Tomography) scanner (or CT scanner) that provides images of a 2-dimensional section of a patient, to be used by medical staff for diagnosis or surgery. Computerized tomography (also referred to as computer tomography or computed tomography) is the combination of mathematics, computer science, physics, and engineering involved in the image reconstruction, typically from several hundred X-rays taken in coplanar directions. Both parallel and point (or fan-beam) X-rays have been used, though modern scanners usually employ the latter. Two pioneers, A. M. Cormack, a physicist, and G. N. Hounsfield, an engineer, were awarded the 1979 Nobel prize in medicine for the "development of computer assisted tomography."
Mathematically, the problem is to reconstruct an unknown density function \(f(x,y)\) describing a 2-dimensional section of an object from its integrals along lines.The main mathematical tool behind computerized tomography is the Fourier transform. It is known that \(f\) can be reconstructed if its integrals along all lines parallel to an infinite set of directions are known, while if the set of directions is finite, then the reconstruction problem does not generally have a unique solution. Worse, in practise only a finite number of line integrals are available and consequently the Fourier inversion process must be discretized. The utility of the entire process rests on the fact that despite the lack of uniqueness, a sufficiently large number of X-rays permits a reconstruction to any desired degree of accuracy. This very short summary is inadequate, since there are a huge number of variations on this theme, necessitated by the many various applications. In addition, there are quite different algorithms based, for example, on linear algebra. The literature is vast. The reader who wishes to learn more could begin with the texts of Epstein [7] and Kak and Slaney [24], both of which are accessible to advanced undergraduate students; Natterer and Wübbeling [31] is set at a slightly higher level.
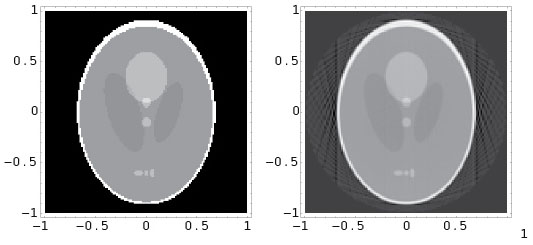
The relation of geometric tomography to computer tomography can be summed up as follows. While geometric tomography focuses entirely on obtaining information about sets (equivalently, density functions taking only 0 or 1 as values), computerized tomography attempts to reconstruct general density functions. On the other hand, while computerized tomography deals only with X-rays, geometric tomography employs other forms of data such as those listed above.
Relation to Discrete Tomography
While there were certainly several results prior to 1994 that can be classified as discrete tomography, a term introduced by Larry Shepp, the subject took off that year at a mini-symposium Shepp organized at DIMACS. The focus of discrete tomography is on the reconstruction of lattice sets, that is, finite subsets of the integer lattice \(\Bbb{Z}^n\), from their discrete X-rays parallel to lattice directions (i.e., directions parallel to vectors with integer coordinates).
Lattice sets are natural models for atoms in a crystal, and the original motivation for discrete tomography came from a genuine application in high-resolution transmission electron microscopy (HRTEM). Indeed, the DIMACS meeting was inspired by work of a physicist, Peter Schwander, whose team developed a technique that effectively allows the discrete X-rays of a crystal to be measured in certain lattice directions parallel to vectors with small integer coordinates. The process is described in detail by Schwander [38]. The algorithms of computerized tomography are useless, since the high energies required to produce the discrete X-rays mean that no more than about three to five discrete X-rays of a crystal can be taken before it is damaged. Discrete tomography has been a very active field since its inception, due to attempts to find suitable algorithms and to the stimulus provided by applications to crystallography and other areas, such as data compression and data security. The books [20] and [21] edited by Herman and Kuba provide an overview of discrete tomography.
Shepp's original vision was that discrete tomography should be concerned with the reconstruction of functions defined on \(\Bbb{Z}^n\) from their integrals along lattice lines, i.e., lines passing through at least two points of \(\Bbb{Z}^n\). This definition allows a clear view of geometric and discrete tomography as overlapping but distinct subjects. Later, Herman and Kuba [21, p. 18] attempted to widen the scope. In their view, discrete tomography is concerned with determining an unknown function \(f\) with a discrete range from weighted sums over subsets of its domain (if the latter is discrete) or from weighted integrals over subspaces (sic) of its domain (if the latter is continuous). According to private communication from Herman and Kuba, this definition was concocted mainly to encompass as many applications as possible. Unfortunately, shifting the emphasis from a discrete domain to a discrete range allows many situations that have essentially nothing to do with discrete mathematics or methods. For example, the problem of determining a star body (or equivalently, its characteristic function) from its section function would become part of discrete tomography! It is more appropriate either to adopt Shepp's definition of discrete tomography, or to generalize it as Herman and Kuba do provided the domain of \(f\) is required to be discrete.